たった1つの数式で3Dのポン・デ・リングを制作した人がすごすぎる！

2017/12/28

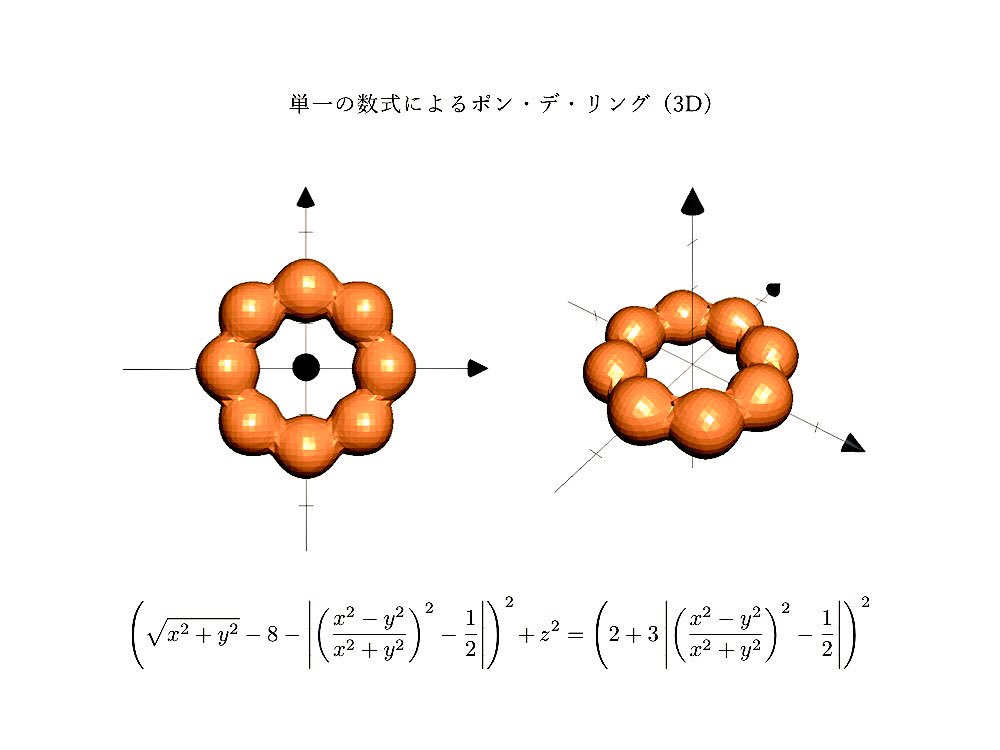
ミスドの看板商品であり、みんなに大人気のポン・デ・リング。
これを、何とたった1つの数式で3Dモデリング化した天才的な人がいた！

本物そっくりな見た目に驚くこと間違いなし！

トピックス

1 1つの数式を用いてポン・デ・リングを3D化

1つの数式を用いてポン・デ・リングを3D化

3時間に及ぶ試行錯誤の末，たった1つの数式で3Dの「ポン・デ・リング」を表示することに成功．(2Dのもあるよ) pic.twitter.com/r23phIA4hp

— CHARTMAN (@CHARTMANq) 2017年12月27日

出典：@CHARTMANq：Twitter

こちらは数式を使ってポン・デ・リングを3Dモデリングした図。
あの八つの丸みを再現するとなると、さぞかし数式も長くなるのでは…と思ったら、たった1つの数式で表現できることが判明！
実際に書かれた数式は確かに一列。
数学に馴染みがなければちんぷんかんぷんだが、とにかく「すごすぎる」としか言えない…！

出典：@CHARTMANq：Twitter

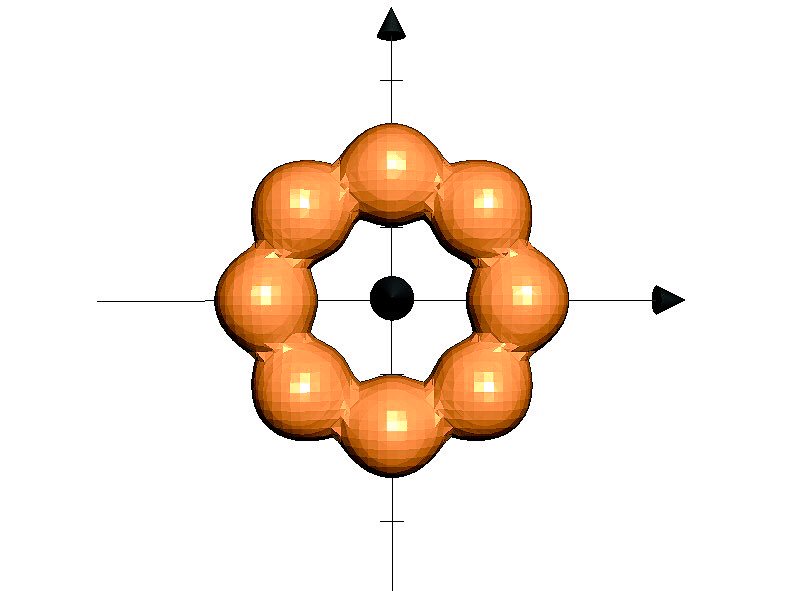
X軸とY軸、そしてZ軸に沿って図式で表したポン・デ・リング。
モコモコした形と、ツヤツヤした表面が本物そっくりで美味しそう🍩

出典：@CHARTMANq：Twitter

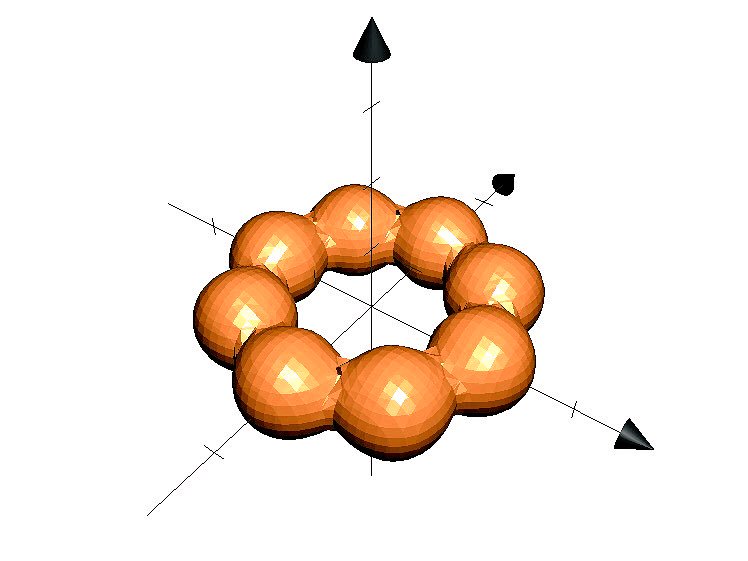
斜めに傾けてみると、よりリアリティを感じられる。
繋ぎ目もバッチリ作られていてすごい！

2Dの領域は，極座標を用いて

(r-2|cos4θ|-10)(r+|cos4θ|-6)≤0

と表されます．こっちはかなりシンプルですね(^-^)

— CHARTMAN (@CHARTMANq) 2017年12月28日

出典：@CHARTMANq：Twitter

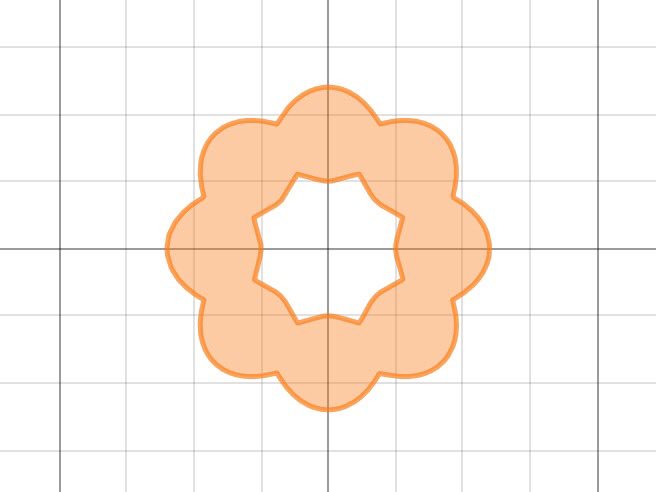
そしてこちらは2Dで表した図。
方眼紙のような図面にポン・デ・リングの図形が描かれており、式も3Dよりは短くてシンプル。
2Dも3Dもちゃんとポン・デ・リングだと一目でわかる形をしていて、まさに天才的！

他にストロベリー・リングやフレンチクルーラーも制作

(グフゥ，食べたくなってしまったではないですかストロベリー・リング) pic.twitter.com/7QwK1wmVzX

— CHARTMAN (@CHARTMANq) 2017年12月28日

1年半以上前に作ったものでよければ，こちらをとうぞ( ´▽｀)

ただ，これは1つの数式で表されるわけではなく，楕円面を並べたにすぎません． pic.twitter.com/7aXSGkNvuM

— CHARTMAN (@CHARTMANq) 2017年12月28日

何と同じ要領で、ストロベリー・リングやフレンチクルーラーの3Dモデリングまで作っていた！
ストロベリー・リングにはピンク色のストロベリーソースがかかっており、フレンチクルーラーもエッジが利いててお見事✨
何だかミスドに直行したくなってきた٩(๑￫◡￩๑)۶

「3Dモデルって全部数式で作られてる？」リプとツイ主のやり取り

よい質問ですね．

2Dで考える→3Dに拡張
という手順で作りましたが，2Dでの作業中は極座標を用いていました．
3Dに拡張する際，自分が既に知っていたxyz系のトーラス面(最も単純なドーナツ形のものです)の方程式を利用したかったため，xyzに変換して完成させた次第です．

— CHARTMAN (@CHARTMANq) 2017年12月27日